此篇需要二叉树基本知识,若对二叉树不了解,请移步一篇文章搞懂二叉树!
Welcome back!
在了解了二叉树的基本知识后,我们知道,二叉树虽然可以在一般情况下控制比较次数在logN内结束,但是一旦遇到较差的情况,导致树的高度很高的时候,性能就不是很令人满意了。另外,对于插入过程中保持二叉树的完美动态平衡这一操作,代价又显得太高了。所以,我们稍微放松点完美平衡的要求,将操作的性能保持在logN内完成即可。
下面,在正式学习红黑二叉树之前,我们先学习另一种树形结构“2-3查找树(B-树)”。这种树形结构也是红黑二叉树形成的历史由来,掌握它非常简单,并且能更好的帮助我们理解红黑二叉树。
2-3查找树
2-3查找树只是高级数据结构B-树中非常简单的一种情况。之前二叉树中了解到,操作的复杂度与树的高度成正相关。那么在如何维持树的高度和平衡性,我们这里需要一些灵活性。
- 我们允许二叉树中的一个结点保存多个键值
- 我们将标准二叉树中的结点(1个键值)称之为2-结点。
- 我们将含有2个键值和3个连接线(连接子结点)的称之为3-结点。
一个2-3查找树或是一个空树,或是由下列结点组成:
- 2-结点:含有1个键与2条连接线的结点,其与标准二叉树的结点性质一样,x.left < x < x. right。
- 3-结点:含有2个键与3条连接线的结点,其中左连接线都小于2个键,中连接线在2个键之间,右连接线都大于2个键。

- 一个完美的2-3平衡树,它的所有空链接到根节点的距离应该是相同的。
2-3树 查找 get:
设查找的键为key,查找的节点为x。与二叉树相似:
- 若未命中,则返回null。
- 若 key < x.key , 在x的左子树中寻找。
- 若 key > x.key , 在x的右子树中寻找。
- 若结点x是2-结点,则与二叉树一样。
- 若结点是3-结点,则比较key与2个键的大小,看是直接命中还是在哪个连接线继续寻找。

2-3树 插入 put:
- 先进行一次未命中查找。如果命中,则替换value。如果没有命中,则创建新结点挂在树的底部。
向2-结点 h 中插入
直接挂在树的底部会有些问题,破坏了树的平衡性,我们想要保持插入也是平衡的,所以选择结点上变化。那么分两种情况:
- 如果h无子结点或h的子结点是2-结点,则与二叉树一样插入,2-结点变3-结点。

- 如果h的子结点是3-结点,则3-结点变成4-结点了。(见下)
向3-结点 h 中插入
- 如果向只含有一个3-结点的树插入,则3-结点变4-结点。这个情况则需要稍微变形处理下,可以将4-结点转化为2个2-结点。
规定:4-结点中有3个键,4个连接线。中间的键可以提到上面,成为左右两个键的父结点,此时树的高度+1。由于变换的是根节点,依然维持了完美平衡性。

理解树的变化是非常重要的,这关乎2-3树如何成长。
- 如果向父结点为2-结点的3-结点 h插入(接上),则3-结点变4-结点。变换后,提上来的中间键与父结点合并,注意,此时仍要保持父结点内键的大小顺序。

- 如果向父结点为3-结点的3-结点 h插入,则子结点变为4-结点,变换后父结点也变为4-结点,则再次向上变换,直至没有4-结点。

- 如果插入的路径向上全是3-结点,则我们的根节点变为临时的4-结点,此时我们可以向情况1.中所描述的处理,分解4-结点,树的高度+1。

请注意,2-3树中任何4-节点的分解与转化,均是局部操作,不会影响到树的平衡性!
只要符合相应的形态,变换即可进行。
2-3树 性能:
2-3树的高度必然在 (logN)/(log3) ~ logN 之间,故增删查改的性能也在 O[ (logN)/(log3) ]~ O( logN ) 之间。
OK,2-3树的介绍就到这里,代码没写,因为我们的重点不是2-3树,而是红黑树。现在我们离红黑树只差一句话的距离了。当然,在告别2-3树之前,我们再看一眼2-3树的完美身影 :) 。
(喝口水,休息一下)
红黑二叉查找树
首先,让我们来去掉3-结点,就从2-3树变成了红黑树。
本质上,红黑树就是利用标准二叉树中结点的额外信息表示2-3树。所以,红黑树是一个二叉树,或者说,红黑树是二叉树的子类(不太准确的说法)。
去掉3-结点
上面说的结点的额外信息,其实就是指的(结点)链接的颜色。在标准二叉树中,所有链接的颜色都是黑色,而在红黑树中,我们规定有红色和黑色两种链接。
注:不少教科书上都是用结点为红/黑来定义红黑树,这里采用的是另一种定义规则,并不冲突。
- 黑链接是2-3树中的普通链接,也是标准二叉树中的链接。
- 红链接是将两个2-结点,变为一个3-结点。
所以,我们只需要将3-结点还原成由红链接连接的2个2-结点,即可去掉3-结点!而对于3-结点的子结点,则分配给两个2-结点来完成。
等价定义
我们这里为了方便讨论情况,不影响性质的前提下,定义以下规则:
一个静态的红黑树:(不需要再变换的、操作完成后的)
- 所有红链接均为左链接
- 没有任何一个结点与两个红链接相连
- 该树是完美黑色平衡的,即任意空结点到根结点的路径上黑链接数量相同!(黑链数目既是树的高度)
肯定有小朋友对上面三条规则不满的,这边我来解释一下:
- 前提是变换好的红黑树。
- 红链接为右链接可不可以,我说可以,但是为了统一和美观,以及减少讨论的情况和复杂度,我们统一规定左边。
- 为啥不能两个红链接相连?两个红链接相连其实就产生了4-结点,这在2-3树中是会被转化的,而我们红黑树是由2-3树演变而来,所以应该通过相应的转化变换解决这个问题,后面会有介绍方法,且听我细细说来。
- 因为完美平衡二叉树是黑色平衡的,所以我们红黑也是完美黑色平衡的。或者等会你就能明白,为什么我们不计入红色为树的高度了,看下面。

- 注意这里红链接横置后的连接顺序,没有改变
我们将红黑树中,所有的红链接都横过来画(或者说,将2-3树中所有3-结点内部都加上红链接),即显示了为何红黑树也是2-3树,并且红黑树的高度就是2-3树的高度,也就是空结点到根节点路径上普通黑链接的数量。
- 红黑树既是二叉树,也是2-3树。
所以我们在红黑树中可以使用2-3树高效的插入算法,以及二叉树中高效的查找算法。
结点构成及颜色表示
boolean RED = trueboolean BLACK = false
我们在二叉树的基础上,加入了结点的颜色来表示指向当前结点的链接颜色。

1 | private class Node { |
旋转 rotate:
为了将我们所有的红链接都能自由的左右旋转,于是有以下两个方法:假设结点为 h
向左旋转 rotateLeft:
左旋可以将红链从右边移至左边。
这个方法多数用于删除操作和调整树的平衡,以满足我们的等价定义。

当然从视觉上来看就是h 的右子结点不动,h 自己旋转至左下方,同时,交换子结点和红链。
- 旋转后需要重置父结点的链接。
- 旋转后需要调整结点的大小,因为结点的高度变化了。
1 | private Node rotateLeft(Node h) { |
向右旋转 rotateRight:
右旋可以将红链从左边移至右边。
这个方法多数临时用于删除操作中,后面我们会介绍删除操作。

操作与左旋完全相反,不再赘述。
1 | private Node rotateRight(Node h) { |
插入 put:
红黑树的插入是为数不多的比较复杂的实现之一(还有就是删除),联系2-3树,这里我们先分情况讨论:
- 规定:插入的新结点的color都是RED
这个只要想想2-3树中插入就明白了。
向单个2-结点中插入新键:
如果一个红黑树只有一个2-结点,即根节点root,那么插入的时候会有三种情况:
- key == root,替换root 的值。
- key < root,则插入左子结点,此时不需要调整。
- key > root,则插入右子结点,此时为了满足等价定义,
rotateLeft()一下就好了。
向树底部的2-结点插入新键:
和上面三个情况差不多,只要保证我们的等价定义,以及二叉树的基本定义(x.left < x < x.right),调整并更新父链接就好啦。
向一个双键树(3-结点)插入新键:
分以下三种情况:
1. 新插入的键最大:
插入右子结点x.right。则形成4-结点,此时需要进行变换。这里介绍一个flipColors方法,用来分解4-结点:
- 一个键h 的左右子结点都是红色,h 为黑色。
- 将h 的左右子结点都变为黑色,h 变为红色。
- 此时树的高度+1。
- 调整后的h 可以根据其他情况进行继续变换。


1 | private Node flipColors(Node h) { |
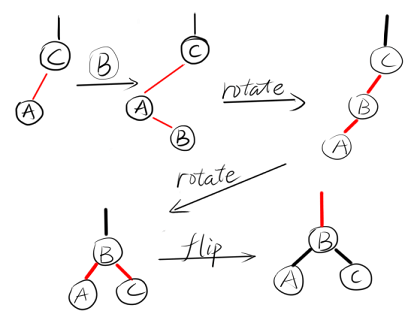
2. 新插入的键最小:
插入左子结点的子结点 x.left.left,则此时形成连续的左链接都是红色(A 插入 B-C ,形成 A-B-C)。
这时候需要我们先对C进行**右旋 rotateRight(C)**,然后就形成了上面1.的情况。
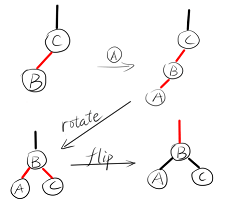
3. 新插入的键大小在两个键之间:
插入左子结点的右结点 x.left.right,这种情况最为复杂。例如B插入A-C
此时需要先对A进行**左旋 rotateLeft(A)**,然后就形成了上面2.的情况。
- 由此我们可以看出,插入总是在“ 情况3 -> 情况2 -> 情况1 ”之间转化。
- 请确保完全理解了上述中树的变化,再继续看下去。
根节点总是黑色
当我们进行插入后,根节点有时候会变为红色,此时当根节点由红色转为黑色时,树的高度+1。
代码实现:
插入的实现,可以参考2-3树,这里只是在插入完成后,重新调整树的结构以达到完美平衡,满足等价定义。
1 | public void put(Key key, Value value) { |
删除 delete:
删除任意一个键,是红黑树中最为复杂的算法。而在删除任意结点的时候,我们先想想二叉树中是如何进行删除操作的。
当x不是树的末结点,若直接删除会造成空缺,树不连续,我们需要变换一下。
则当x不是树的末结点且x有两个子结点时:
删除x后,需要寻找x的右子结点中最小的(或者x的左子结点中最大的)来代替x的位置,保证二叉树的性质“每个结点的键都大于任意左子节点而小于任意右子节点”。
故我们可以这样理解,最复杂的情况下,假设x不是树的末结点且x有两个子结点:
如果我们将x先和右结点最小的(或者左结点最大的)进行交换,然后就将x变为树的末结点,此时即可直接删除。
所以,删除的操作可以简化为 删除最小值 或 删除最大值 的操作。
删除最小值 deleteMin:
由二叉树性质可知,最小键一定是在树的最左边。并且由等价定义可知,最小值一定是在树的末端最左边。
当我们进行删除末结点的时候,让我们先回归2-3树,并且稍微允许临时4-结点的存在。
- 有时候为了让父结点变为红色,需要临时合并为4-结点。
- 如果删除的末结点是3-结点,则直接删除即可。
- 如果删除的末结点是2-结点,直接删除会破坏树的完美平衡。所以此时我们需要进行变换。
分以下几种情况:
- 如果此时要删除的结点,它的父结点、兄弟结点(父结点的右结点)都是2-结点,则可以将这三个结点
flipColors,还原为一个临时的4-结点。这样在我们删除后,依然是3-结点,不会破坏完美平衡,高度-1。
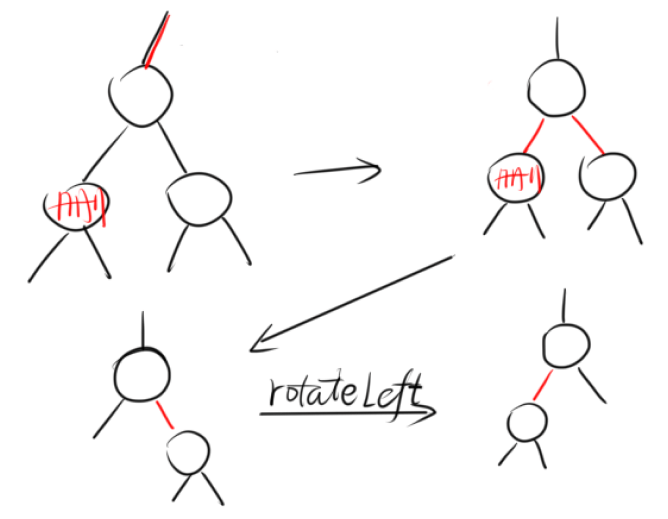
如果它的父结点不是红色,则想办法变为红色。
- 如果此时要删除的结点,它的父结点是2-结点,而它的兄弟结点不是2-结点,则此时需要向兄弟结点借一个结点过来,形成3-结点。
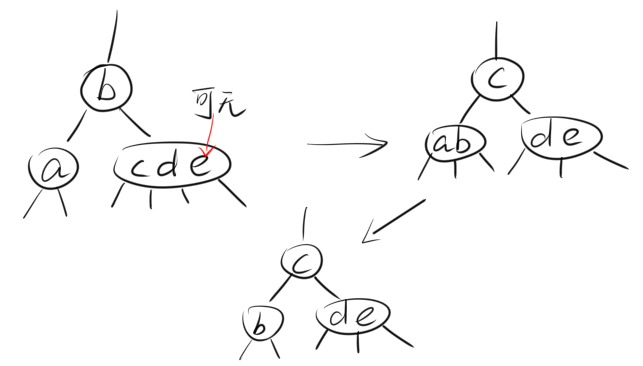
- 如果此时要删除的结点,它的父结点不是2-结点,那么从父结点借一个结点过来,形成3-结点。
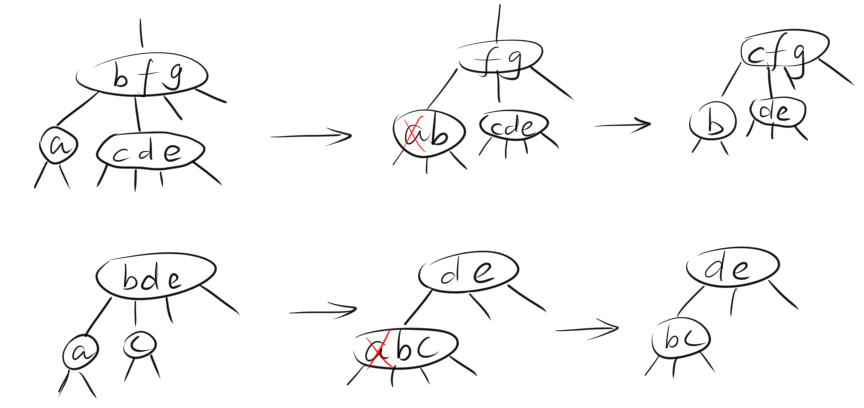
若兄弟结点不是2-结点,则从父结点借一个结点后,兄弟结点可以补给父结点一个最小的结点,保持树的完美平衡性。
若兄弟结点是2-结点,则父结点中最小的结点向下合并,形成临时4-结点。
待删除完成后,需要自下而上重新整理树的结构,将所有的临时4-结点分解,从而满足我们的等价定义。
代码实现:
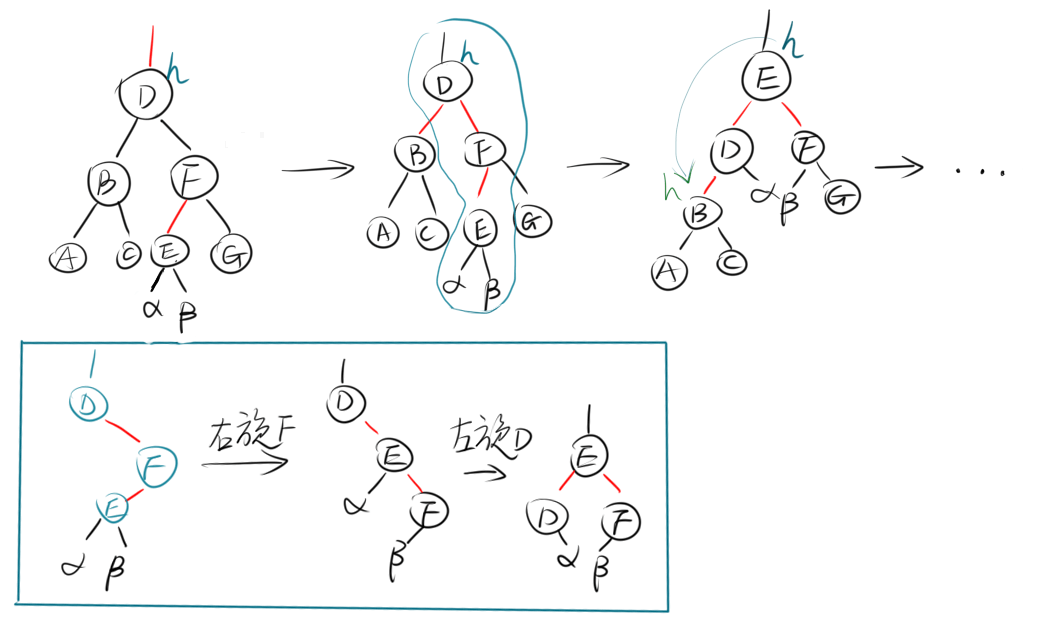
沿着树的最左路径,一路向下的过程中,当遇到2-结点,实现一些变换
moveRedLeft(),从而保证当前结点不是2-结点。
这里也就是想办法变红色,从而能够删除键而不破坏树的完美平衡。
1 | private Node moveRedLeft(Node h) { |
1 | public void deleteMin() { |
一开始,如果根节点的两个子键都没有红键,则需要我们临时将根节点变红,从而可以拆分出红键。
而在删除完成最后,如果树还有结点,则要将根节点还原为黑色,以满足根节点总是黑色。
其中balance()方法与之前我们进行put后的操作类似,不再赘述。
1 | private Node balance(Node h) { |
删除最大值 deleteMax:
由于我们的红链都是左链,所以这里与deleteMin稍有不同。
沿着树的最右路径,一路向下的过程中,当遇到2-结点,实现变换
moveRedRight(),从而保证当前结点不是2-结点。
1 | private Node moveRedRight(Node h) { |
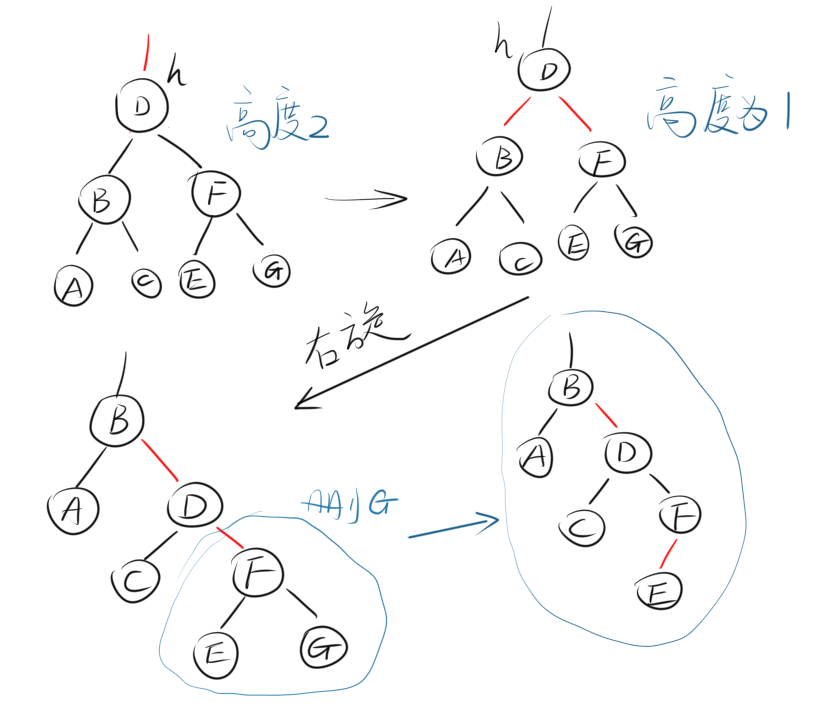
如图示不难理解,由于我们删除的是最大值,所以键一定在右子结点中,故要将红键从左往右传递。其与操作与deleteMin差不多,就不赘述了。但是要记住,我们这些局部的旋转和移动都不会改变树的组成(见2-3树性质)。
1 | public void deleteMax() { |
删除任意结点的实现:
删除任意结点就是转为为删除最小值和删除最大值的操作。
1 | public void delete(Key key) { |
上面这段代码就不解释了,和之前deleteMin的原因一样。我们主要看下面的具体实现。
1 | private Node delete(Node h, Key key) { |
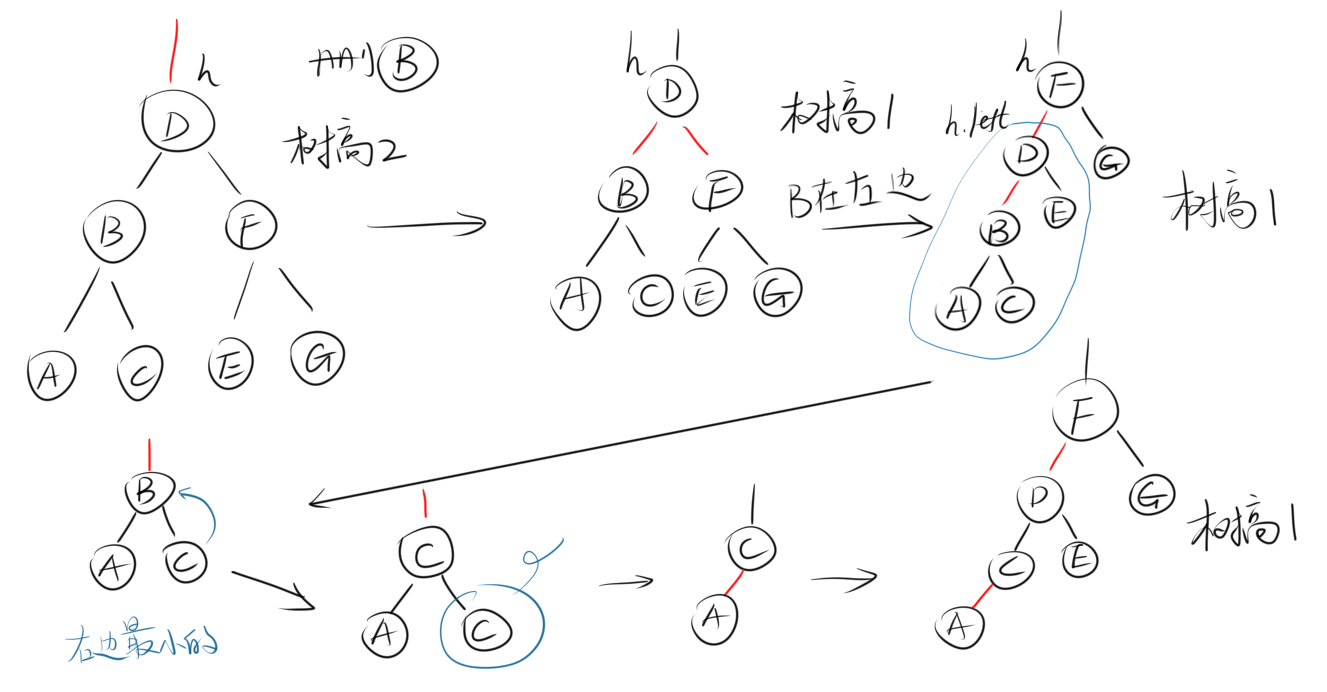
- 如果寻找的键在左边,则消除左边路径上的2-结点,参考
deleteMin。 - 如果寻找的键在右边,则消除右边路径上的2-结点,参考
deleteMax。 - 我们在这里主要采用的是寻找右子键中最小值来交换自己的位置,此时待删除结点就从树的中间部分被交换到了树的末端,从而删除右子键中的最小值,简化为删除最小值的问题。
- 最后也要记得自下而上整理整个树的结构,满足我们的等价定义。
性能:
- 无论我们如何插入键值,红黑树都是几乎完美平衡的。
这个可以通过我们2-3树的性质得到。
- 大小为N的红黑树的高度不会超过2logN。
所以其操作复杂度始终维持在 **~O(logN)**。一般来说,想构建2logN高度的红黑树比较困难,需要最左边一条路径均是3-结点,而其他的子结点都是2-结点才可以。我们在一般数据里很少能遇到。
- 大小为N的红黑树,根节点到任意子结点的平均路径长度为 ~1.00logN
这个性质很容易得到。而红黑树相对于二叉树而言,我们提高了40%以上的性能,能够使任何操作都在 ~O(logN) 内完成。
结束语:
复杂的红黑树终于了解完了,可以看出,理解2-3树对于掌握红黑树的原理至关重要。在树的生长变换中,局部变换并不会改变整体的结构这一点非常重要,也是红黑树的灵魂。
在另一篇文章,将会带来Java中最常用的数据结构——散列表。
谢谢观看。
参考文献:《算法导论》 《Algorithms, 4th Edition》